30. Définition d'une fonction
- Description
- Ressources
- Activité
Par définition, une fonction est une règle de correspondance qui associe à une valeur x de la variable indépendante au plus une valeur y de la variable dépendante. À partir de représentations graphiques, il est généralement possible de repérer les fonctions:: il suffit de s’assurer qu’aucune droite verticale tracée sur le graphique n’a plus d’une intersection avec la courbe.

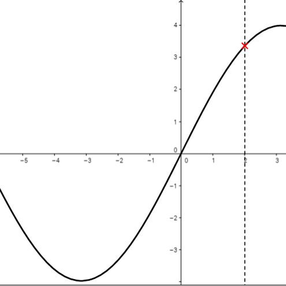
1. Déterminez la nature de la courbe qui vous est présentée. Représente-t-elle une fonction ? Au besoin, faites afficher la droite verticale et déplacez-là à l’aide de votre curseur avant de répondre à la question. Appuyez sur « Nouveau graphique » et répétez l’exercice pour chacune des courbes qui vous seront présentées.
2. Arrêtez-vous sur une courbe qui représente bel et bien une fonction. Cochez la case « droite verticale » et déplacez la droite à l’aide de votre curseur. Que remarquez-vous ?
3. Arrêtez-vous sur une courbe qui ne représente pas une fonction. Cochez la case « droite verticale » et déplacez la droite à l’aide de votre curseur. Que remarquez-vous ?
4. Pour qu’une courbe ne représente pas une fonction, la droite verticale doit-elle toujours avoir plus d’un point d’intersection avec la courbe ?
5. Pour une courbe de votre choix, positionnez la droite verticale en x = 1. Dans la règle de correspondance qui est représentée, à combien de valeur(s) y de la variable dépendante est associée la valeur x = 1 de la variable indépendante ?
6. Imaginez-vous qu’on trace une droite horizontale sur une des courbes présentées. Si cette droite avait, à un certain endroit, plus d’un point d’intersection avec la courbe, devrait-on conclure que cette courbe ne représente pas une fonction ?
1. Déterminez la nature de la courbe qui vous est présentée. Représente-t-elle une fonction ? Au besoin, faites afficher la droite verticale et déplacez-là à l’aide de votre curseur avant de répondre à la question. Appuyez sur « Nouveau graphique » et répétez l’exercice pour chacune des courbes qui vous seront présentées.
2. Arrêtez-vous sur une courbe qui représente bel et bien une fonction. Cochez la case « droite verticale » et déplacez la droite à l’aide de votre curseur. Que remarquez-vous ? Réponse: Peu importe où on la place, la droite verticale n’a soit aucun, soit un seul point d’intersection avec la courbe. Il n’y a aucun autre cas possible.
3. Arrêtez-vous sur une courbe qui ne représente pas une fonction. Cochez la case « droite verticale » et déplacez la droite à l’aide de votre curseur. Que remarquez-vous ? Réponse: On trouve nécessairement des endroits où la droite verticale a plus d’un point d’intersection avec la courbe. Sur l’un des graphiques, on peut même placer la droite verticale de sorte à trouver trois points d’intersections avec la courbe.
4. Pour qu’une courbe ne représente pas une fonction, la droite verticale doit-elle toujours avoir plus d’un point d’intersection avec la courbe ? Réponse: Non, il suffit que cela n’arrive qu’une fois pour que la courbe ne puisse correspondre à la représentation d’une fonction.
5. Pour une courbe de votre choix, positionnez la droite verticale en x = 1. Dans la règle de correspondance qui est représentée, à combien de valeur(s) y de la variable dépendante est associée la valeur x = 1 de la variable indépendante ? Réponse: Le nombre de valeur(s) y de la variable dépendante correspond au nombre de point(s) d’intersection qu’a la courbe avec la droite verticale.
6. Imaginez-vous qu’on trace une droite horizontale sur une des courbes présentées. Si cette droite avait, à un certain endroit, plus d’un point d’intersection avec la courbe, devrait-on conclure que cette courbe ne représente pas une fonction ? Réponse: Non, car une fonction peut associer deux valeurs x de la variable indépendante à une même valeur y de la variable dépendante.