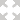29. Équation quadratique
- Description
- Ressources
- Activité
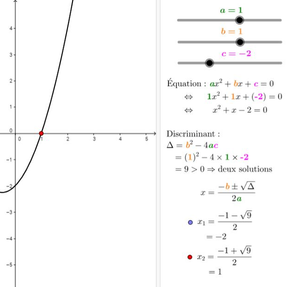
Contrairement à la fonction linéaire, la fonction quadratique peut présenter différents cas en ce qui a trait au nombre de zéros : elle peut en admettre deux, un seul ou aucun. À vous de voir de quelle manière se traduit chacune de ces situations dans l’utilisation de la formule quadratique, lorsque vient le temps de trouver le(s) zéro(s).

1. Posez a = -3, b = -2 et c = 1.
a) Combien de zéro(s) cette fonction admet-elle ?
b) Par conséquent, que peut-on dire du discriminant ?
c) Donnez la valeur exacte de chaque zéro de cette fonction.
2. Posez a = 1, b = -4 et c = 4.
a) Combien de zéro(s) cette fonction admet-elle ?
b) Par conséquent, que peut-on dire du discriminant ?
c) Attribuez des valeurs aux paramètres a, b et c de façon à obtenir une parabole qui n’admet aucun zéro. Que peut-on alors dire du discriminant ?
3. Peut-on procéder de la même façon qu’aux numéros précédents pour trouver le(s) zéro(s) de f(x) lorsque a = 0 ?
4. Soit une fonction quadratique d’équation f(x) = ax2 + bx + c. Si le sommet de la parabole est tel que sa coordonnée en y est strictement négative, que peut-on dire des paramètres a, b et c si la fonction…
a) Admet deux zéros ?
b) N’admet aucun zéro ?
c) N’admet qu’un seul zéro ?
1. Posez a = -3, b = -2 et c = 1.
a) Combien de zéro(s) cette fonction admet-elle ? Réponse: Deux zéros.
b) Par conséquent, que peut-on dire du discriminant ? Réponse: Le discriminant est positif.
c) Donnez la valeur exacte de chaque zéro de cette fonction. Réponse: x1 = -1 et x2 = 1/3.
2. Posez a = 1, b = -4 et c = 4.
a) Combien de zéro(s) cette fonction admet-elle ? Réponse: Un seul.
b) Par conséquent, que peut-on dire du discriminant ? Réponse: Le discriminant est nul.
c) Attribuez des valeurs aux paramètres a, b et c de façon à obtenir une parabole qui n’admet aucun zéro. Que peut-on alors dire du discriminant ? Réponse: Le discriminant est négatif.
3. Peut-on procéder de la même façon qu’aux numéros précédents pour trouver le(s) zéro(s) de f(x) lorsque a = 0 ? Réponse: Non, car on n’a plus une équation quadratique, mais linéaire.
4. Soit une fonction quadratique d’équation f(x) = ax2 + bx + c. Si le sommet de la parabole est tel que sa coordonnée en y est strictement négative, que peut-on dire des paramètres a, b et c si la fonction…
a) Admet deux zéros ? Réponse: Peu importe les valeurs de b et c, on a nécessairement que a > 0.
b) N’admet aucun zéro ? Réponse: Peu importe les valeurs de b et c, on a nécessairement que a < 0.
c) N’admet qu’un seul zéro ? Réponse: Cela est impossible étant donné que la coordonnée en y du sommet est strictement négative.