28. Représentations d'un intervalle
- Description
- Ressources
- Activité
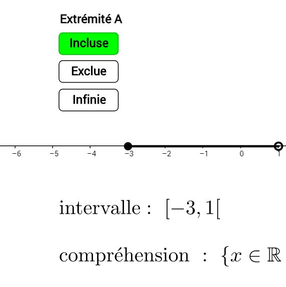
Un intervalle peut être représenté de plusieurs façons: notation utilisant les crochets, définition en compréhension ou représentation visuelle par un segment de droite sur un axe horizontal. Utilisez les boutons associés aux extrémités A et B (Incluse, Exclue et Infinie) pour créer des intervalles et comprendre les liens entre leurs différentes représentations.

1. À l’aide des boutons associés aux extrémités A et B (Incluse, Exclue et Infinie), recréez les intervalles suivants :
a) [-5;-1[
b) {x ∈ R | -3,1 < x ≤ 0}
c) ]2,7 ; ∞ [
d) {x ∈ R | x > -1,5}
e) R
f) {3 ; 5}
g) R+
2. Recréez l’intervalle ]1,29; 1,30[. À votre avis, combien y a-t-il de nombres réels sur cet intervalle ?
3. Est-il possible qu’un intervalle soit fermé sur une extrémité infinie (ex.: [1, ∞]) ? Comment l’expliquez-vous ?
1. À l’aide des boutons associés aux extrémités A et B (Incluse, Exclue et Infinie), recréez les intervalles suivants :
a) [-5;-1[ Réponse: Extrémité A : Incluse, positionnée en -5 ; Extrémité B : Exclue, positionnée en -1
b) {x ∈ R | -3,1 < x ≤ 0} Réponse: Extrémité A : Exclue, positionnée en -3,1 ; Extrémité B : Incluse, positionnée en 0
c) ]2,7 ; ∞ [ Réponse: Extrémité A : Exclue, positionnée en 2,7 ; Extrémité B : Infinie
d) {x ∈ R | x > -1,5} Réponse: Extrémité A : Exclue, positionnée en -1,5 ; Extrémité B : Infinie
e) R Réponse: Extrémité A : Infinie ; Extrémité B : Infinie
f) {3 ; 5} Réponse: Impossible car {3 ; 5} n’est pas un intervalle. C’est plutôt un sous-ensemble des nombres naturels N qui ne contient que deux nombres : 3 et 5.
g) R+ Réponse: Extrémité A : Exclue, positionnée en 0 ; Extrémité B : Infinie
2. Recréez l’intervalle ]1,29; 1,30[. À votre avis, combien y a-t-il de nombres réels sur cet intervalle ? Réponse: Il y en a une infinité, comme sur tout intervalle dont les extrémités a et b ont des valeurs différentes. Le fait que l’intervalle soit fermé, ouvert ou semi-ouvert n’y change rien.
3. Est-il possible qu’un intervalle soit fermé sur une extrémité infinie (ex.: [1, ∞]) ? Comment l’expliquez-vous ? Réponse: C’est impossible : les symboles ∞ et -∞ représentent respectivement l’infini et moins l’infini, qui ne sont pas des nombres réels. Ils ne peuvent donc pas appartenir à l’intervalle, car celui-ci est un sous-ensemble des nombres réels.