32. Réciproque d'une fonction
- Description
- Ressources
- Activité
Graphiquement, on peut obtenir la réciproque de la fonction f, notée f(-1), en intervertissant les coordonnées de tous les points de la courbe représentant la fonction f. Dans ce contexte, peut-on se représenter la courbe de f(-1) à partir de celle de f ? Pour le savoir, observez chaque fonction présentée dans cette animation ainsi que sa réciproque.

. Sélectionnez une fonction au hasard et cochez la case « Points ». Déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Comparez-le au point appartenant à f-1(x) (en bleu). Que pouvez-vous en dire ?
2. Cochez la case « Axe de symétrie » et déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Selon cet axe de symétrie, qui correspond à la droite y = x, à quoi correspond la réflexion du point appartenant à f(x) ?
3. Cochez la case « Afficher/masquer la trace » et déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Par rapport à l’axe de symétrie, que représentent tous les points bleus obtenus ?
4. Cochez la case « Réciproque » pour voir complètement la courbe représentant f-1(x).
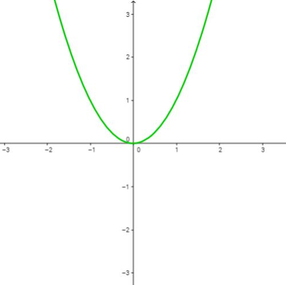
5. Cliquez sur « Autre fonction » jusqu’à ce que vous obteniez f(x) = x2, puis manipulez l’animation.
a) À votre avis, la réciproque de f(x) = x2 est-elle une fonction ? Justifiez votre réponse.
b) Quel ajustement peut-on faire à la fonction f(x)=x2 pour que sa réciproque soit une fonction ?
6. Parmi celles qui sont présentées dans l’animation, y a-t-il une autre fonction dont la réciproque n’est pas une fonction lorsqu’on ne limite pas son domaine ?
. Sélectionnez une fonction au hasard et cochez la case « Points ». Déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Comparez-le au point appartenant à f-1(x) (en bleu). Que pouvez-vous en dire ? Réponse: La coordonnée en x du point appartenant à f(x) correspond toujours à la coordonnée en y du point appartenant à f-1x, et vice-versa.
2. Cochez la case « Axe de symétrie » et déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Selon cet axe de symétrie, qui correspond à la droite y = x, à quoi correspond la réflexion du point appartenant à f(x) ? Réponse: La réflexion du point appartenant à f(x) (en vert) correspond au point appartenant à f-1(x) (en bleu).
3. Cochez la case « Afficher/masquer la trace » et déplacez le point appartenant à f(x) (en vert) à l’aide de votre curseur. Par rapport à l’axe de symétrie, que représentent tous les points bleus obtenus ? Réponse: Ils représentent l’ensemble des réflexions des points appartenant à f(x).
4. Cochez la case « Réciproque » pour voir complètement la courbe représentant f-1(x).
5. Cliquez sur « Autre fonction » jusqu’à ce que vous obteniez f(x) = x2, puis manipulez l’animation.
a) À votre avis, la réciproque de f(x) = x2 est-elle une fonction ? Justifiez votre réponse. Réponse: Sa réciproque n’est pas une fonction, car il arrive que deux valeurs de y correspondent à la même valeur de x.
b) Quel ajustement peut-on faire à la fonction f(x)=x2 pour que sa réciproque soit une fonction ? Réponse: On peut limiter son domaine à l’intervalle x ∈ [0,∞[. Ainsi, l’image de f-1(x) correspond aussi à [0,∞[ (en bleu sur le graphique), et f-1(x)est telle qu’il n’y a jamais plus d’une valeur de y correspondant à chaque valeur de x.
6. Parmi celles qui sont présentées dans l’animation, y a-t-il une autre fonction dont la réciproque n’est pas une fonction lorsqu’on ne limite pas son domaine ? La fonction f(x) = sin x.